首页
博客
首页
博客

接雨水

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

初步思路

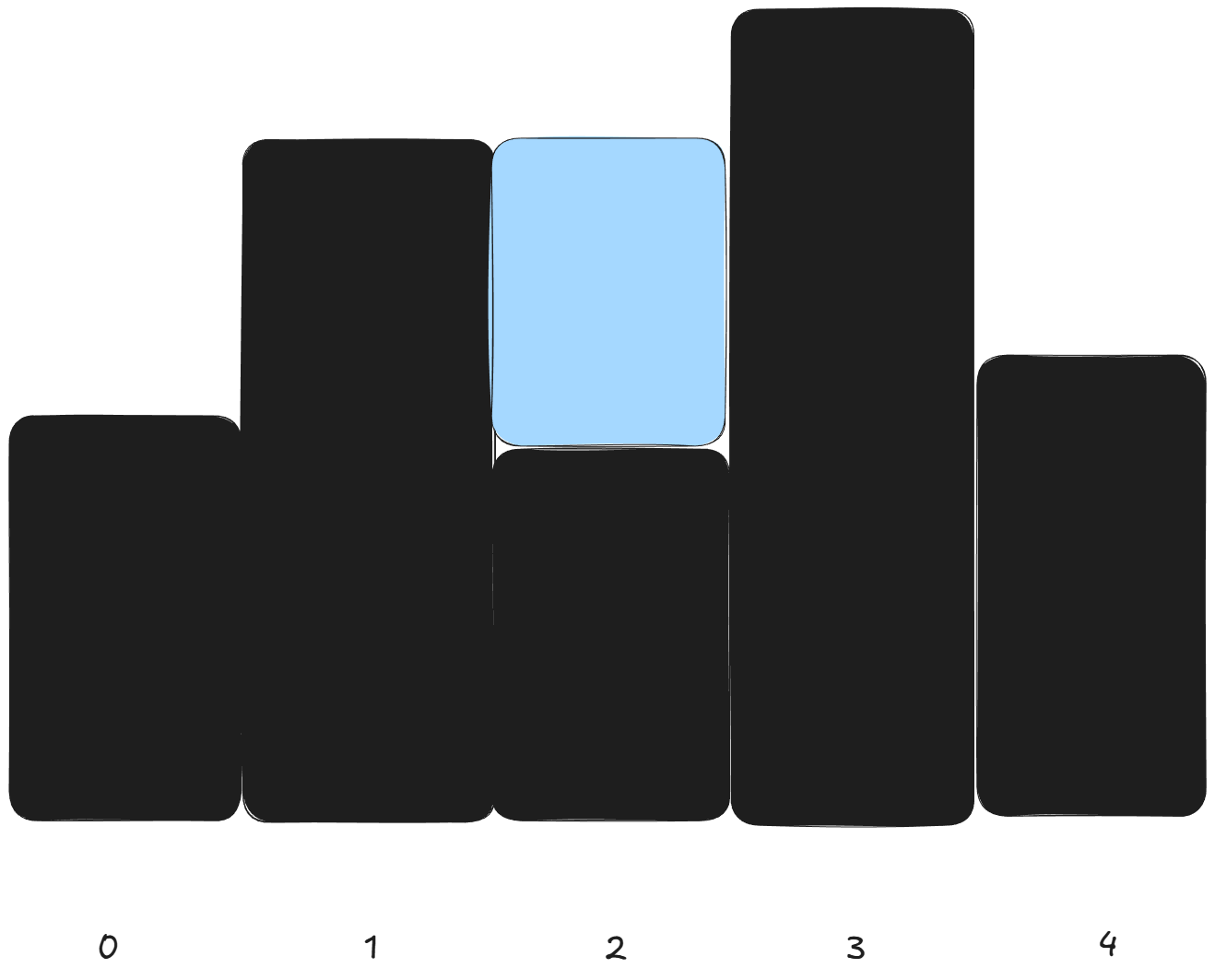
这里我们只关注2号柱子可以接的雨水，可以看到它接的雨水的大小为 在它之前的柱子的最高高度与在它之后的柱子的最高高度的最小值减去它的高度

这里初步的思路就已经形成了

记 lmax[i]为 [0,i] 的最高高度，rmax[i]为 [i,n-1] 的最高高度

则 对于某一处i所能接的雨水的大小为min(lmax[i-1],rmax[i+1])-height[i]

特别的，对于i==0和i==n-1的情况，它俩所能接的雨水固定为0，不用考虑

所以可写出代码

1func trap(height []int) int {
2    n := len(height)
3
4    lmax,rmax := make([]int,n),make([]int,n)
5
6    lmax[0],rmax[n-1] = height[0],height[n-1]
7
8    for i:=1;i<n;i++ {
9        lmax[i] = max(lmax[i-1],height[i])
10    }
11
12    for i:=n-2;i>=0;i-- {
13        rmax[i] = max(rmax[i+1],height[i])
14    }
15
16    ans := 0
17    for i:=1;i<n-1;i++ {
18        if height[i]<min(lmax[i-1],rmax[i+1]) {
19            ans += min(lmax[i-1],rmax[i+1])-height[i]
20        }
21    }
22
23    return ans
24}

优化空间复杂度

考虑这么一件事，如果lmax[i-1]小于rmax[i+1]，那么i处所能接的雨水为lmax[i-1]-height[i]，

那如果lmax[i-1]小于rmax[j]（i+1 <= j <= n-1）,还可以推出i处所能接的雨水为lmax[i-1]-height[i]吗？

其实是可以的，因为如果lmax[i-1]小于rmax[j]，则一定可以推出lmax[i-1]小于rmax[i+1]，所以是可以的；那么同理如果rmax[i+1]小于lmax[j]（0 <= j <= i-1）可以推出i处能接的雨水为rmax[i+1]-height[i]

所以我们其实可以设置双指针 l 和 r，分别指向0和n-1，同时设置两个变量lmax和rmax分别记录[0,l]和[r,n-1]的高度的最大值。如果lmax < rmax，则可以确定l处所能接的雨水为lmax-height[l]，同时右移l；如果rmax < lmax，则可以确定r处所能接的雨水为rmax-height[r]。

ok,我们就可以写出代码

1func trap(height []int) int {
2    n := len(height)
3
4    l,r := 0,n-1
5
6    lmax,rmax := height[0],height[n-1]
7
8
9    ans := 0 
10
11    for l<r {
12        lmax = max(lmax,height[l])
13        rmax = max(rmax,height[r])
14
15        if lmax<rmax {
16            ans += lmax-height[l]
17            l++
18        }else {
19            ans += rmax-height[r]
20            r--
21        }
22    }
23
24    return ans
25
26
27}
页面导航